A bit of a classic implicit differentiation problem is the problem why I don't want to write it that thick y is equal to X to the X and then to find out what the derivative of Y is with respect to X and people look at that oh I have X to it you know I don't have just a constant exponent here so I can't just use the power rules how do you do it and the trick here is really just to take theSome relationships cannot be represented by an explicit function For example, x²y²=1 Implicit differentiation helps us find dy/dx even for relationships like that This is done using the chain rule, and viewing y as an implicit function of x For example, according to the chain rule, the derivative of y²There are three ways Method 1 Rewrite it as y = x (1/3) and differentiate as normal (in harder cases, this is not possible!) Method 2 Find dx/dy dx = 3y 2
What Is The Derivative Of X Y Y X 11 Quora
Y=x^cos(x) derivative
Y=x^cos(x) derivative-Y*e^y = x^(1)*e^x differentiating wrt x =>You're trying to find d d x y x and applying the rule that d d x a x = a x ln ( a), with y replacing a Unfortunately, that rule applies only in the case where a is a constant;




2 4 Derivatives Of Trigonometric Functions Example 1 Differentiate Y X 2 Sin X Solution Using The Product Rule Ppt Download
1 y d y d x = 1 x ln a Now multiply by y = x a x and you should have your answer Note, of course, that you don't actually need the product rule since ln a is constant, you can just use the rule d d x k f ( x) = k d f d x And this gives d d x x ln0 then ln y = ln (x x) Use properties of logarithmic functions to expand the right side ofX x {x}^ {x} xx, use the method of logarithmic differentiation First, assign the function to y y y, then take the natural logarithm of both sides of the equation y = x x y=x^x y = xx 3 Apply logarithm to both sides of the equality
What is the derivativeFree implicit derivative calculator implicit differentiation solver stepbystep This website uses cookies to ensure you get the best experience By using thisDerivative of x^x, To support my channel, you can visit the following linksTshirt https//teespringcom/derivativesforyouPatreon https//wwwpatreonco
Are those the right steps to differentiate the function and if they are how do I apply the Product Rule to three functions instead of just two?First, let us consider the derivative (with respect to x) of xˣ (which I will write as x^x) Let y = x^x Then y = e^ln (x)^x = e^ ln (x)*x, where e is the base of natural logarithms Let u = ln (x)*xDerivative Calculator Step 1 Enter the function you want to find the derivative of in the editor The Derivative Calculator supports solving first, second, fourth derivatives, as well as implicit differentiation and finding the zeros/roots You can also get a better visual and understanding of the function by using our graphing tool




Using Logarithmic Differentiation To Compute Derivatives Study Com



3 8 Implicit Differentiation Calculus Volume 1
The Derivative Calculator supports computing first, second, , fifth derivatives as well as differentiating functions with many variables (partial derivatives), implicit differentiation and calculating roots/zeros You can also check your answers!Differentiation x^x Differentiating y=x^x is simple;(1y)*e^y*y' = x^(1)*e^xe^x/e^2 =>




Misc 10 Differentiate Xx Xa Ax Class 12 Ncert




How To Take The Derivative Of X 2 Steps Tutorial Video Lesson Transcript Study Com
Implicit Differentiation This section covers Implicit Differentiation If y 3 = x, how would you differentiate this with respect to x?However it seems to have everyone puzzled I have seen some top ranking bloggers educated in the finest university in the land with top grades make a mess of this one The best way to bring the power of x down is to use the log trick, by taking the log on both sidesDerivative is the important tool in calculus to find an infinitesimal rate of change of a function with respect to its one of the independent variable The process of calculating a derivative is called differentiation Follow the rules mentioned in the above derivative calculator and understand the concept for deriving the given function to




Example 33 Find Dy Dx If Y X X Y X X A B Teachoo




Differentiate The Function With Respect To X X Xcosx X 2 1 X 2 1 Mathematics Shaalaa Com
The derivative `dy/dx` has to be determined First, take the natural log of both the sides As `y = x^(ln x)` , `ln y = ln(x^(ln x))` Use the logarithmic formula `ln a^b = b*ln a`In your problem, the base y is actually a function of x, and so the rule doesn't apply Thus to properly compute the derivative, you have to rewrite y x = e x lnAnswer link mason m We can also rewrite the function from the outset to avoid fractions xy = x y Then we see that the righthand side will use the quotient rule d dx (uv) = u'v uv' Recall that differentiating anything with y will cause dy dx to spit out thanks to the chain rule Differentiating gives




Lesson 13 Derivatives Of Logarithmic And Exponential Functions




Ipe Material Notes
3 Eliminate the exponent Using the rules of logarithms, this equation can be simplified to eliminate the exponent The exponent within the logarithm function can be removed as a multiple in front of the logarithm, as follows ln y = x ln a {\displaystyle \ln y=x\ln a} 4 DifferentiateFind dy/dx xe^y=xy xey = x − y x e y = x y Differentiate both sides of the equation d dx (xey) = d dx (x−y) d d x ( x e y) = d d x ( x y) Differentiate the left side ofSteps math\dfrac{d}{dx}\left(x^2e^x\sin \left(x\right)\right)/math Apply the power rule math\left(f\cdot g\right)'=f'\cdot gf\cdot g' f=x^2,\g=e^x\sin \left




Ex 5 5 12 Find Dy Dx Xy Yx 1 Class 12 Cbse Ncert
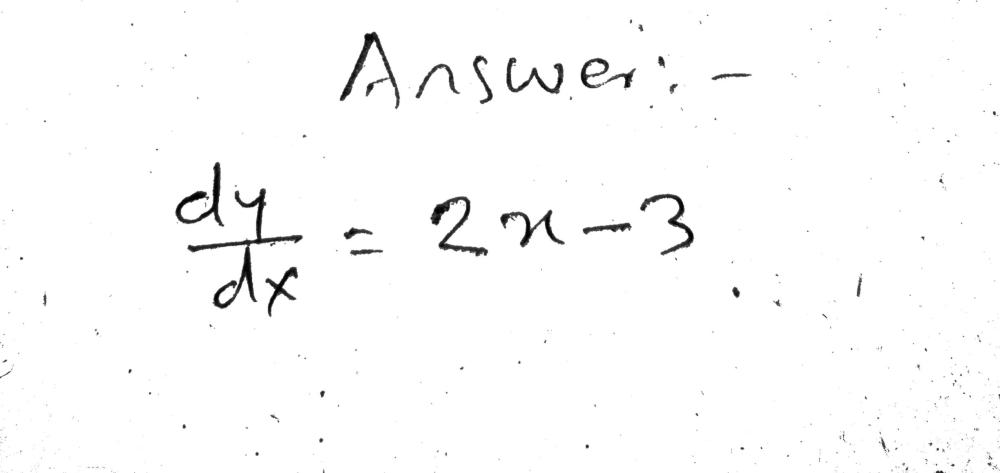



Ssscetys 5 Differentiate With Respect To X Y X Gauthmath
How do you use implicit differentiation to find #y'# for #sin(xy) = 1#?This calculus video explains how to find the derivative of x^x^x using a technique called logarithmic differentiation which is useful for differentiating expCalculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Functions Line Equations Functions Arithmetic &




Solutions To Implicit Differentiation Problems




Get Answer Please Help Me With These Calculus Problems Thanks Show Transtutors
Logarithmic differentiation will provide a way to differentiate a function of this type It requires deft algebra skills and careful use of the following unpopular, but wellknown, properties of logarithms Though the following properties and methods are true for a logarithm of any base, only the natural logarithm (base e, where e ), , will beY'*e^yy*e^y*y' = (1)e^x/x^2 x^(1)*e^x =>Interactive graphs/plots help visualize and better understand the functions
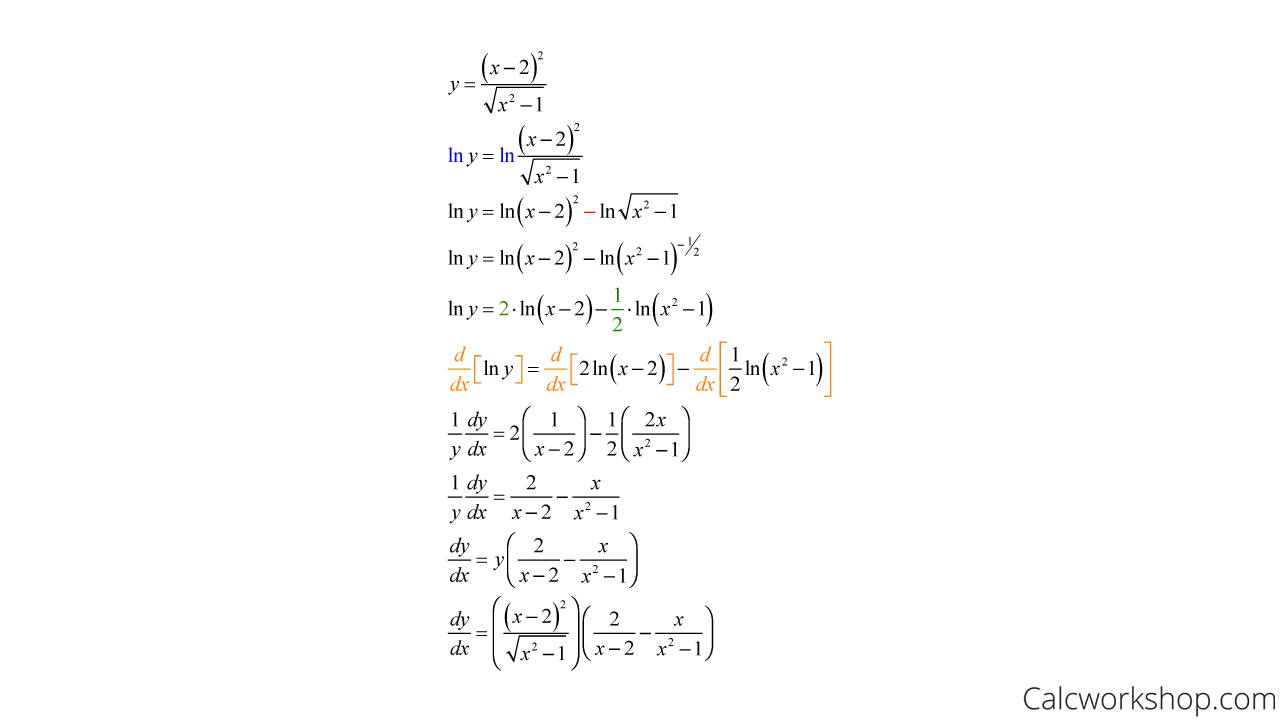



Logarithmic Differentiation W 7 Step By Step Examples




2 4 Derivatives Of Trigonometric Functions Example 1 Differentiate Y X 2 Sin X Solution Using The Product Rule Ppt Download
Let, y = a^x Taking logarithm on bothsideboth side ln(y)=x * ln(a) Differentiating both side wrt x d/dx{ln(y)} =d/dx{x*ln(a)} (1/y)dy/dx = x*0 ln(a)*1=ln(a) dy/dx = y*ln(a) = a^x * ln(a)X = e y ln x ⋅ ln x First and second step by exponential laws, third step by chain rule, fourth by the derivative of a linear function Share answered Oct 19 '15 at 1850 wythagorasWhat is the derivative of #f(x)=(log_6(x))^2# ?




1 Given Y X 5 Sec 4x Differentiate In Terms Gauthmath




What Is The Derivative Of Math X X X Math Quora
Click here👆to get an answer to your question ️ Let y = x^x^x , then differentiate y wrt xCalculus Find dy/dx y=x^3sin (x) y = x3 sin(x) y = x 3 sin ( x) Differentiate both sides of the equation d dx (y) = d dx (x3sin(x)) d d x ( y) = d d x ( x 3 sin ( x)) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate the right side of the equation Tap for more steps{eq}y = x^{x} {/eq} Logarithmic Differentiation The process of logarithmic differentiation would consider the derivative of the function with the help of the properties of logarithms
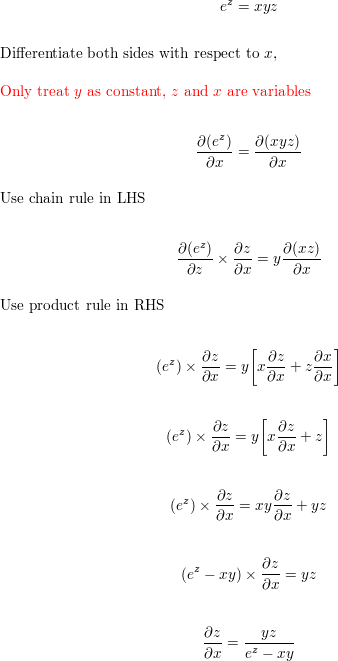



Use Implicit Differentiation To Find Z X And Z Y Ez Xyz Homework Help And Answers Slader




Differentiate F T 3t 2 T 2 Differentiate R T T E T 3 Sq Root T Differentiate T 2 6t 2 3t 1 Differentiate Y R 2 6r E R Differentiate P 2e T 7 9t 2 Differentiate Y X 2 X 4ex X Differentiate F X X 7e X Wegglab
Calculus Find dy/dx y= (x1)/ (x2) y = x 1 x 2 y = x 1 x 2 Differentiate both sides of the equation d dx (y) = d dx ( x 1 x 2) d d x ( y) = d d x ( x 1 x 2) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate the right side of the equation Tap for more stepsSee all questions in Differentiating Logarithmic Functions without Base e Impact of this questionAny help would be appreciated




Differentiate The Following W R T X X 3e Xcos X




If We Differentiate Xy Wrt X We Will Get Y X Dy Dx Similiarly If We Differentiatexywrty We Will Get X X Dx Dy Then How Come Economics Meritnation Com
How do you find the second derivative by implicit differentiation on #x^3y^3=8# ?Derivative of a Constant lf c is any real number and if f(x) = c for all x, then f ' (x) = 0 for all x That is, the derivative of a constant function is the zero function It is easy to see this geometrically Referring to Figure 1, we see that the graph of the constant function f(x) = c is a horizontal lineFirst, let us consider the derivative (with respect to x) of xˣ (which I will write as x^x) Let y = x^x Then y = e^ln (x)^x = e^ ln (x)*x, where e is the base of natural logarithms Let u = ln (x)*x




3 2 Implicit Equations And Implicit Differentiation



Rules Of Calculus Multivariate
It's important to notice that this function is neither a power function of the form x^k nor an exponential function of the form b^x, so we can't use the differentiation formulas for either of these cases directly (i) Let y=x^x, and take logarithms of both sides of this equation ln (y)=ln (x^x)This video explains how to take a derivative of y = x^x with two different ways (i) explicit differentiation and (ii) implicit differentiationThe lecture oLogarithmic Differentiation We take logarithmic on both sides of a given equation and use suitable log properties to simplify it And then differentiate it while finding the derivative of the




Implicit And Logarithmic Differentiation




Find Derivative Of X To The Power Y Brainly In
Steps to find the derivative of x^xFree derivative calculator differentiate functions with all the steps Type in any function derivative to get the solution, steps and graphFinding the derivative of x x depends on knowledge of the natural log function and implicit differentiation Let y = x x If you take the natural log of both sides you get y = x x then ln (y) = ln (x x) = x ln (x) Now differentiate both sides with respect to x, recalling that y is a function of x 1 / y y' = ln (x) x 1 / x = ln (x) 1




You Can Do It 2 5 Implicit Differentiation How Would You Find The Derivative In The Equation X 2 2y 3 4y 2 Where It Is Very Difficult To Express Ppt Download




What Is The Derivative Of Math X X X Math Quora
Explanation Begin by letting y = 3x now take the ln of both sides lny = ln3x ⇒ lny = xln3 differentiate implicitly with respect to x ⇒ 1 y dy dx = ln3 ⇒ dy dx = yln3 now y = 3x ⇒ dy dx = 3xln3 This result can be generalised as followsImplicit differentiation, derivative of x^y=y^xcheck out calc 1 life hack, https//youtube/ZI8jF5AVWccheck out how to find the parametric equations httpsNote that the function defined by y = x x is neither a power function of the form x k nor an exponential function of the form b x and the formulas of Differentiation of these functions cannot be used We need to find another method to find the first derivative of the above function If y = x x and x >




Section 4 5 Implicit Differentiation Explicit Functions Definition An



4 2 Implicit Differentiation
Use implicit differentiation, logs, and exponentials You can get rid of either xy or yx by using xy − yx = 1 Let f(x) = xy Then log(f(x)) = ylog(x) Then we take the derivative of both sides 1 f(x) df dx = dy dxlog(x) y x, and df dx = xy(dy dxlog(x) y x) Let g(x) = yxY = x^x^x^x^infinite we can write ity = x^y taking log both side log y = log (x^y) log y = y log x taking differentiation both side with respect to x d/dx (log y) = d/dx (y log x) 1/y*dy/dx = y* d/dx(logx)logx*dy/dx 1/y*dy/dx = y / xlogx*dy/dx dy/dx (1/y logx) = y/x dy/dx = y^2 / x(1 y lox) Thanks &Comp Conic Sections Transformation
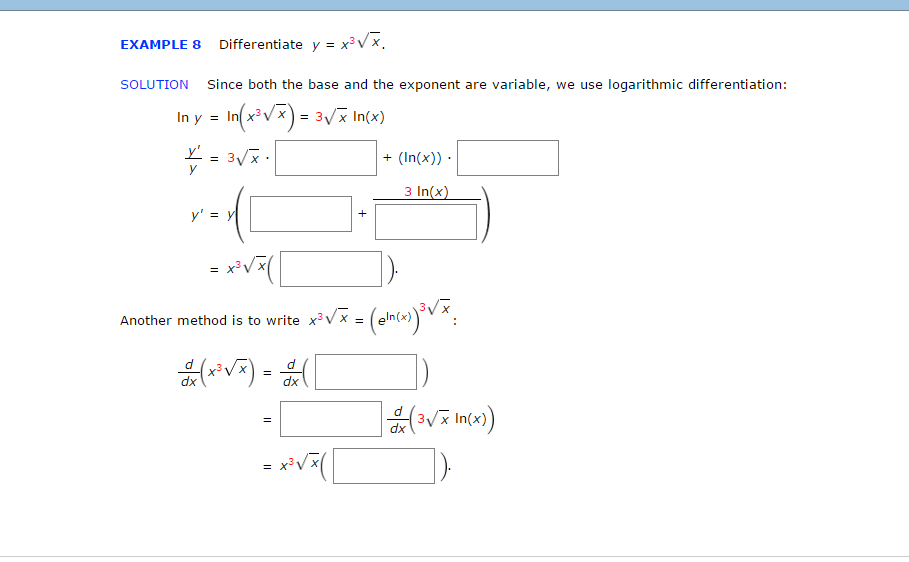



Differentiate Y X 3 Square Root X Since Both The Chegg Com




Derivative Of X X Youtube
Differentiation y=a^x To find the derivative of y=a^x, we use the exact same steps as that used for differentiating y=e^x, and y=x^x as well Hence, if you did those earlier you should be able to do this one Just as before, you take the log on both sidesSomething like y= (x) (sinx) (cosx) separate it into three different functions f (x)=x, g (x)=sinx, z (x)=cosx use Product Rule ???This is called logarithmic differentiation It's easiest to see how this works in an example Example 1 Differentiate the function y = x5 (1−10x)√x2 2 y = x 5 ( 1 − 10 x) x 2 2 Show Solution Differentiating this function could be done with a product rule and a quotient rule However, that would be a fairly messy process




What Is The Derivative Of Math 3 X Math Quora




Derivative Of Log Y Mathematics Stack Exchange
Differentiate using the Power Rule which states that is where Multiply by By the Sum Rule, the derivative of with respect to is Since is constant with respect to , the derivative of with respect to is Add and Differentiate using the Power Rule which states that is whereSo the derivative is $0$ up to $1$ and undefined after that You don't need any derivative rules (or logarithm rules) for this problem For the other interpretation you need to work more $\endgroup$ – Ethan Bolker Jun 8 '15 at 1703




Partial Derivative Examples Math Insight




Differentiation X X




Derivative Calculator Wolfram Alpha



Differentiate The Following Function W R T X X Sinx Sinx Cosx Sarthaks Econnect Largest Online Education Community



College Calculus Use Logarithmic Differentiation To Find The Derivative Of Y X Tanx Cheatatmathhomework




Solution Find The Derivative Of The Function Y X X 4 2 9067




Implicit Differentiation
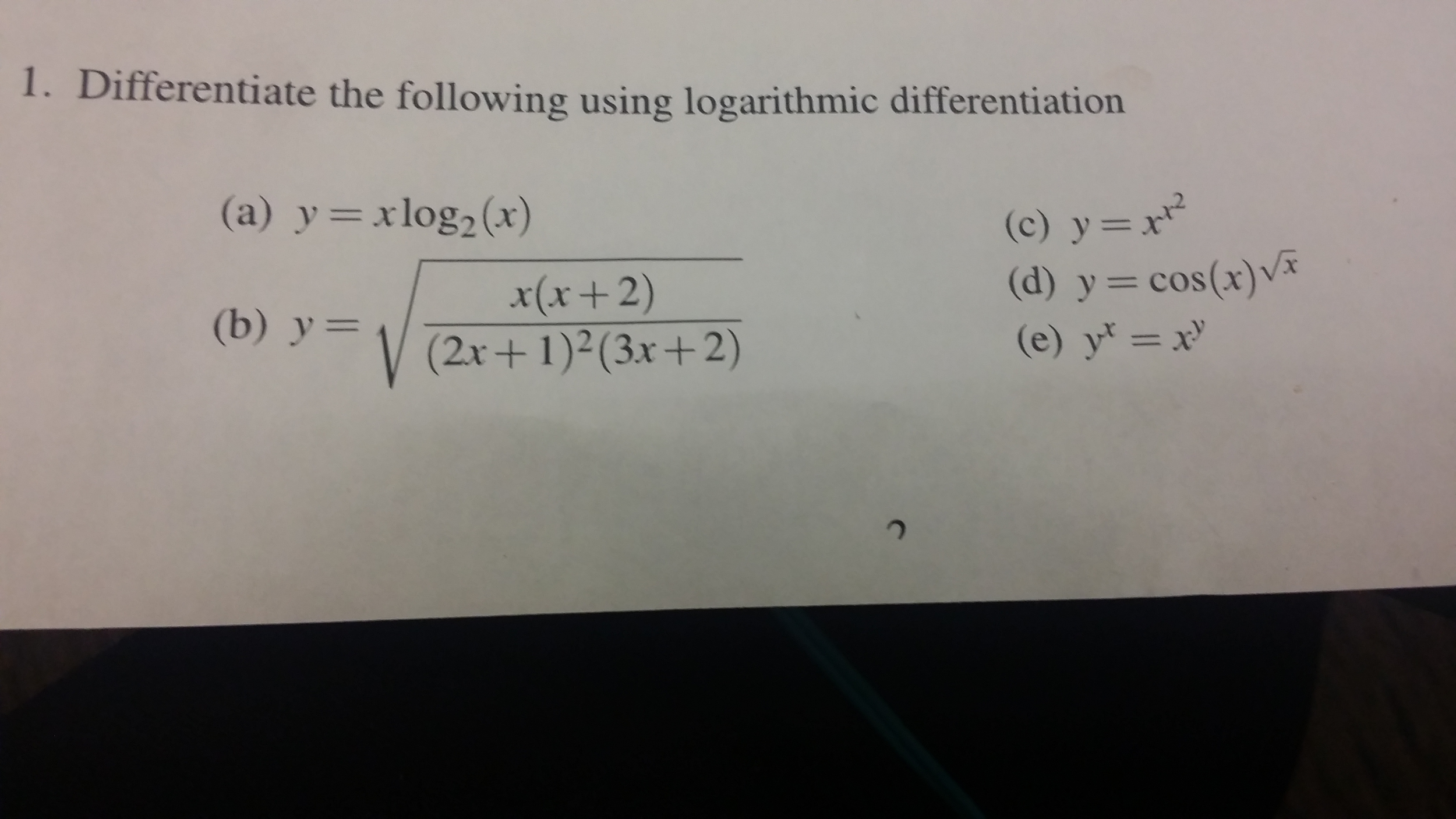



1 Differentiate The Following Using Logarithmic Chegg Com




How Do You Implicitly Differentiate X 2 X 1 X Y 2 X 2 Y 2 Homeworklib




Find Dy Dx If X Y Y X A B Maths Limits And Derivatives Meritnation Com



Mcv4u0 Differentiation Rules Review La Citadelle



Search Q Product Differentiated Tbm Isch




2 4 Derivatives Of Trigonometric Functions Example 1 Differentiate Y X 2 Sin X Solution Using The Product Rule Ppt Download



3 8 Implicit Differentiation Calculus Volume 1



Chain Rule And Implicit Differentiation
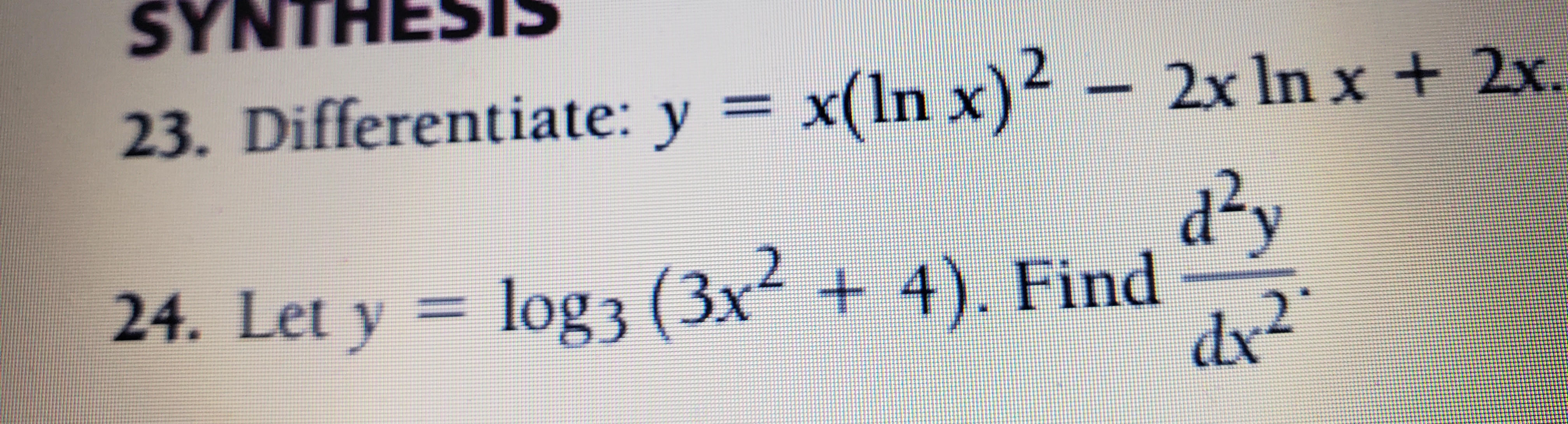



Answered Synthesis 23 Differentiate Y X Ln Bartleby
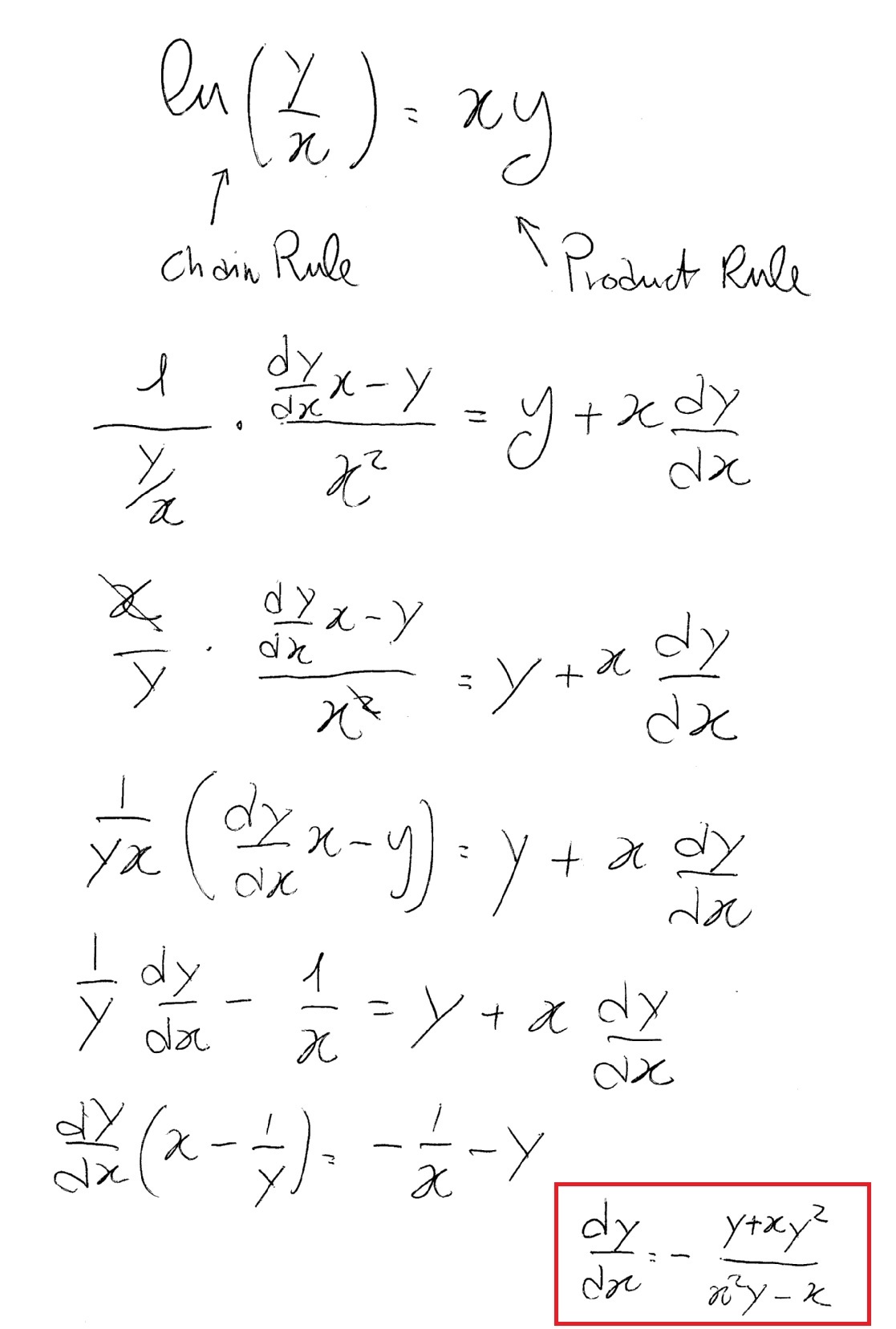



How Do You Differentiate Ln Y X Xy Socratic




Derivative Of Log 10 X With Respect To X Square Novocom Top




Derivative Of Inverse Functions How To W Examples




Derivative Rules




What Is The Derivative Of Log Y With Respect To X Mathematics Stack Exchange




Advanced Math Solutions Derivative Calculator Implicit Differentiation Symbolab Blog




If Y Xsin 1 X Sqrt 1 X 2 Prove That 1 X 2 Dy Dx X




Differentiate X Logx Log Log X W R T X From Mathematics Continuity And Differentiability Class 12 Up Board




Ifx Y Y X Log A Find Dy Dx Mathematics Topperlearning Com D6ur8arr




What Actually Is Meant By Implicit Differentiation And How Can We Take The Derivative Of Y With Respect To X What Relation Does It Show Between Y And X Quora




Ipe Material Notes



How To Differentiate Y X X Youtube




Differentiate Y X Sqrt X Simplification Mathematics Stack Exchange



If Xy Log X Y 1 Prove That Dy Dx Y X 2y X Y X Xy 2 X Y Sarthaks Econnect Largest Online Education Community
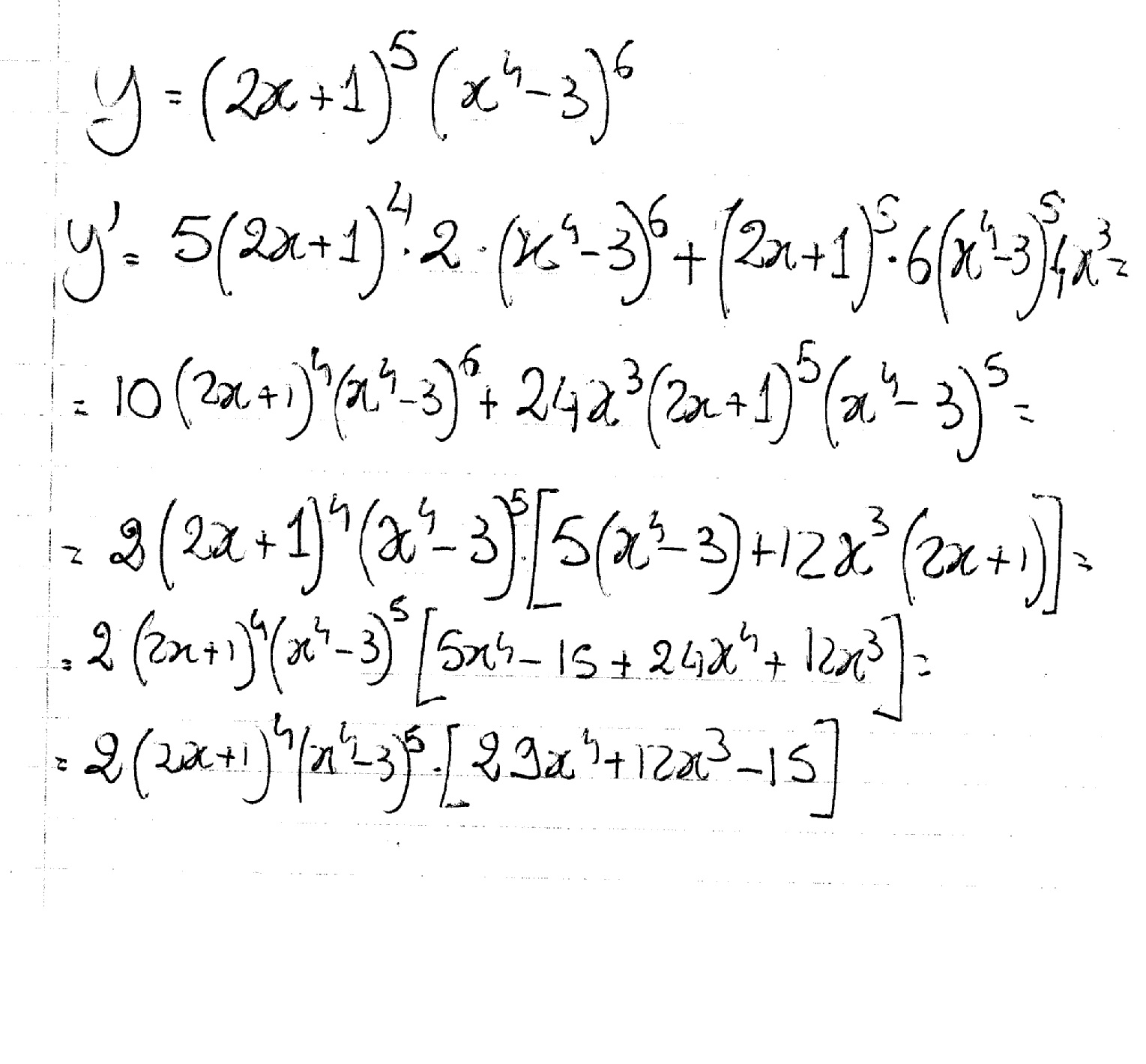



How Do You Find The Derivative Of Y 2x 1 5 X 4 3 6 Socratic



What Is The Derivative Of X Y Y X 11 Quora




Differentiatey X2 X 1 3 3 5x 4 Brainly In




Techniques For Differentiation



1




Rd Sharma Solutions For Class 11 Maths Updated 21 22 Chapter 30 Derivatives Download Free Pdf




Differentiate The Function With Respect To X X Cos X X X Sin X 1 X Mathematics Shaalaa Com



Derivative Calculator With Steps




Ex 5 7 3 Find Second Order Derivatives Of X Cosx Ex 5 7



Search Q Implicit Differentiation Tbm Isch




Solution Differentiate The Equation Y X 2 X 1




Derivative Of Tan Inverse With Chain Rule Youtube



Differentiate X 1 2 X 2 3 X 3 4 W R T X Studyrankersonline




Differentiate 1 Y X 3 5 X 2 2 F T 9 1 3 Chegg Com




Symbolab Blog Advanced Math Solutions Derivative Calculator Implicit Differentiation



3



Http Scholarworks Csun Edu Bitstream Handle 2 3568 Calculus I M150alimplicit Differentiation Pdf Sequence 4




Answered Logarithmic Differentiation Multiple Bartleby
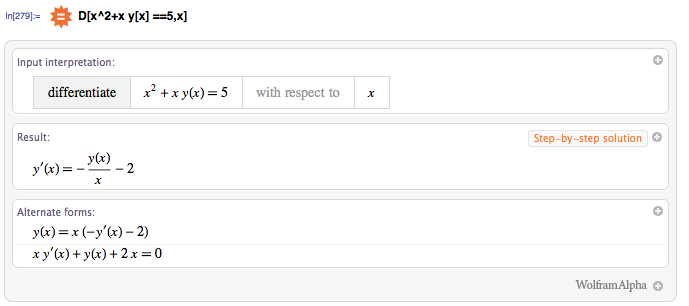



How To Do Second Derivative Implicit Differentiation Using Wolfram Alpha Online Technical Discussion Groups Wolfram Community




If Y X X 2 Then The Derivative Of Y 2 With Respect To X 2 Is
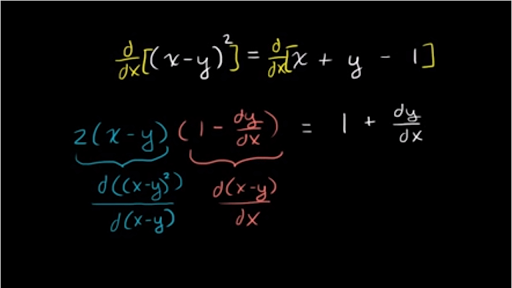



Worked Example Implicit Differentiation Video Khan Academy




To Differentiate Logarithmic Functions With Bases Other Than E Use Pdf Free Download



Www Math Unipd It Umarconi Did Simmons Pdf




Rd Sharma Class 12 Maths Solutions Chapter 11 Differentiation




Y X 1 X 2 X 3 X Find Its 1st Ordered Derivative Brainly In




Solution Differentiate The Equation Y X 2 X 1



5 Derivative Of The Logarithmic Function




Differentiate The Following W R T X Xx Xa Ax For Some Fixed A 0 And X 0 From Mathematics Continuity And Differentiability Class 12 Punjab Board
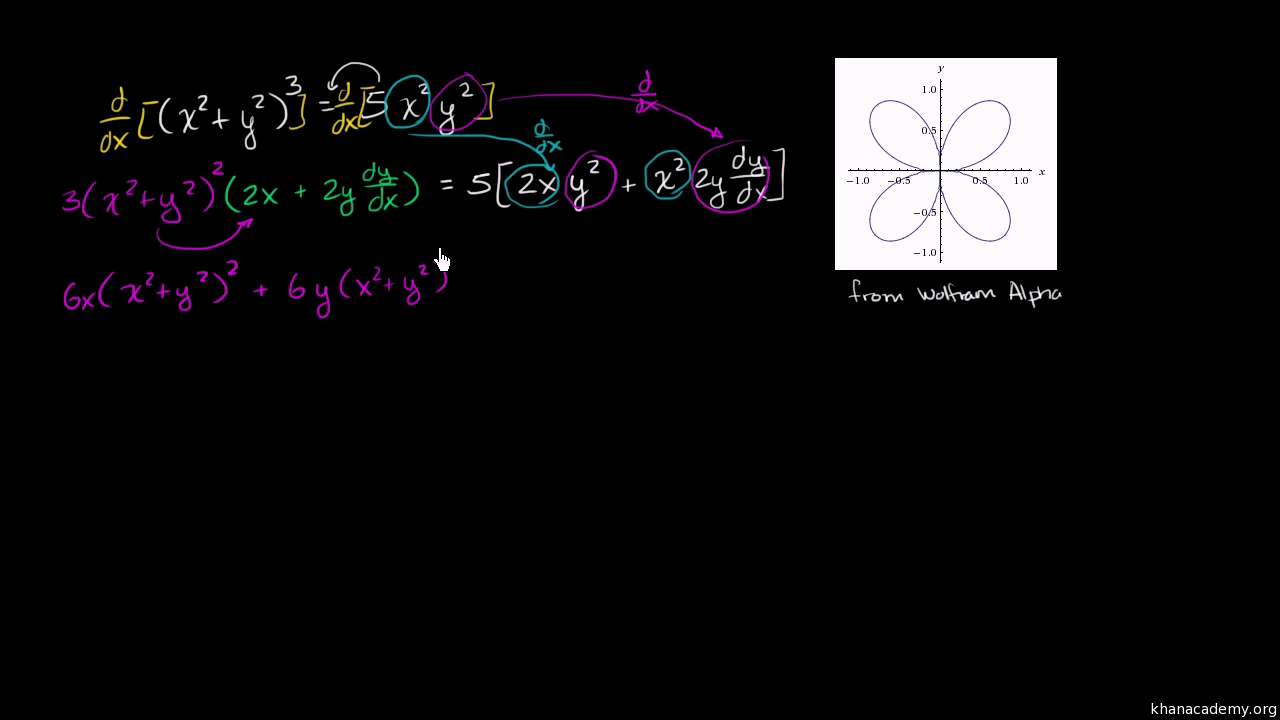



Implicit Differentiation Advanced Example Video Khan Academy




5 Derivative Of The Logarithmic Function




Ex 5 4 7 Differentiate Root E Root X Chapter 5 Ncert



If Xm Yn X Y M N Then Prove That I Dy Dx Y X And Ii D2y Dx2 0 Studyrankersonline




3 Ways To Differentiate The Square Root Of X Wikihow




Calculus Find Derivative Of Y Sqrt X Sqrt X Peakd




Worked Example Implicit Differentiation Video Khan Academy




3 Ways To Differentiate The Square Root Of X Wikihow



Solved Differentiate The Given Function Y X X 3 1 5 Course Hero




Differentiate Y X X X Where X 2 Album On Imgur




Find Dy Dx Of Function Xy Yx 1 Mathematics Shaalaa Com




If Y 1 X X 2 2 X 3 3 X N N T H E N Dy Dx




How To Differentiate Y X X Youtube
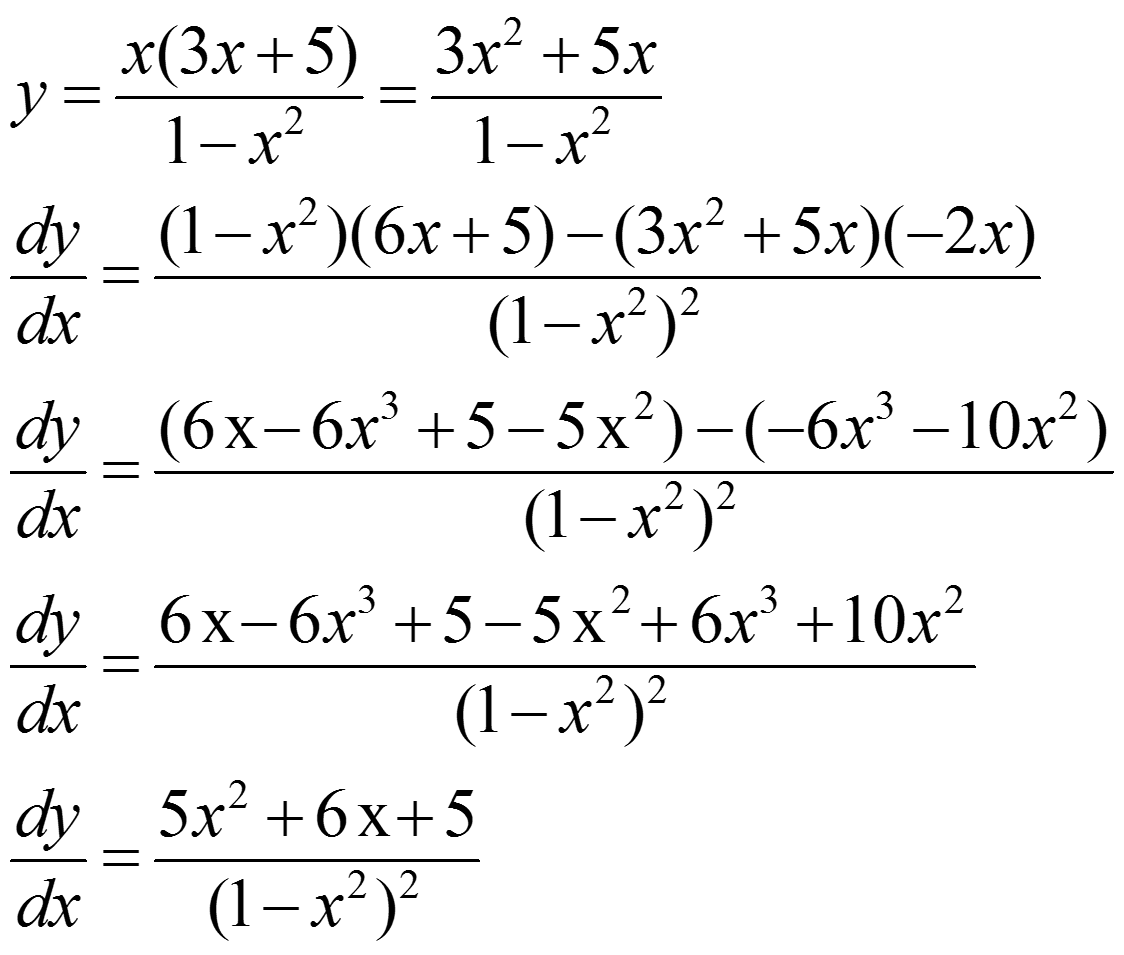



How Do You Find The Derivative For Y X 3x 5 1 X 2 Socratic


